Pigeon Navigation (1): Paths and Probability

How do birds navigate successfully over huge distances from temperate to tropical regions and back every year? How do homing pigeons know how to get back to their owner's loft quickly enough to win a race? Is there some way to control the number of pigeons in Trafalgar Square [or insert your country's pigeon hotspot]?

All good questions. None of which really interest me.

How can we mash up the science of pigeon navigation and a bit of probability theory and come up with something fun and faintly ridiculous? Now you're talking...

For a bit over 10 years now researchers having been attaching GPS devices to the backs of domestic homing pigeons (Columba livia to our classicist friends) before releasing them in more or less odd places. If and when these pigeons make it home, the devices can be removed and we can see exactly where the pigeon has been in the interim (typically at a resolution of a couple of metres, once every second).

This is what a pigeon looks like. Thats a GPS tracker on its back.

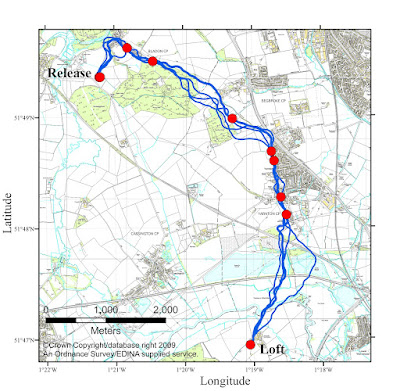A few pigeon paths recorded in the Oxford area. Those red dots sure look exciting don't they? We'll be getting to them eventually...

With such data, our intrepid scientists have shown that probably use landmarks, learn routes home, seem to follow roads and often co-operate in getting home. Sadly, while these findings have revolutionised a popular field of study, been hugely cited and generally proved more than averagely seminal, they didn't include very much probability theory, so I'm going to go ahead and pretty much ignore them from here in.

But where there's data, there's chance to get some machine learning going. So let's get to it...

Paths and Probability


There are many things we might want to learn from the recorded data from the GPS devices. In my research I try to frame learning as a test of various hypotheses using data to adjudicate between them. For example, if we want to learn whether pigeons genuinely follow idiosyncratic routes (which we will) we need to know if the data is more or less likely given this hypothesis than the alternative. If we want to know if the pigeon uses landmarks, we need to find a way to say if the GPS data is more or less likely based on some hypothetical set of landmarks the bird might be using. We need to use probability theory as a link between our data and our theories.

The many recorded locations that a pigeon visits constitute elements of a path that the pigeon actually flies. As with anything probabilistic, we need to start off by finding a way to ask how likely the data (the recorded positions) are. How probable is it that the pigeon flew this path, rather than some alternative route? How can we place probabilities on observations of flight paths?

Well, lets try and get there one step at a time. First I'll just try to give you some idea of the approach we're going to take. In subsequent posts I'll flesh this out with some actual maths.

 If I asked you to place a probability on where the middle of the path (say, the 50th of 100 locations) would be, how would you do it? A reasonable guess would be that on average it would be half way between the release point and the loft. But as the picture above shows, its likely to vary around that point quite a bit. Wherever you think its going to be, you can specify this as a probability distribution, a Gaussian (Normal) distribution, centred on where you think it will be and with a standard deviation that represents your uncertainty.

Now imagine I ask you to put a similar probability on the locations 1/3rd and 2/3rds of the way along the path. We could just as easily make a guess and place Gaussian distributions at both of the points to represent where we think the bird will be. Likely these will be directly 1/3rd and 2/3rds of the way between release and loft. But look at that picture above. If the pigeon starts out to the left of the straight line, its likely to stay out to the left later. So our two locations are going to be correlated, if one is left of centre, the other is likely to be too. They have a joint probability distribution.

The pictures below give some indication how this joint distribution works. We have two correlated variables. Initially we are quite uncertain about both (A). Then we measure one, reducing its uncertainty to zero (B). In addition, the uncertainty in the second variable is reduced, and the expected value moves closer to the first measured value.

(A) Two correlated, unmeasured variables

(B) Variable 1 is measured, variable two is less uncertain

Now, we can extend this to lots of different locations along the path. It is reasonable to imagine that locations will be more correlated the closer they lie along the path. Lets assume we can state a function which we call the covariance function, k(t1, t2), which states how strongly two values (t1, x1) and (t2, x2) should be correlated, and that this gets weaker as the separation of t1 and t2,  dt = |t1-t2| becomes bigger, such as the functions in the figure below.

Correlations get weaker as the difference in t values increases. How fast the correlations decrease depends on the covariance function, k(dt).

Making that assumption, and looking  at 10 points, all jointly distributed, we might get figures like those below

(A) 10 unmeasured variables, correlated according to separation

(B) Measure some variables, others become less uncertain in response.

Going one step further, we might take the number of points we are interested in to infinity, for a continuous path, and then measure just a few of those points

A continuous range of variables, measured in 3 places

What we're getting too, through this exercise, is the concept of a Gaussian process, which is a probability distribution over continuous paths or functions. Much like the Gaussian distribution gives a probability of seeing any number, or set of numbers, a Gaussian process (GP) gives the probability of seeing any path, or any set of points measured on that path. The standard Gaussian distribution can describe any finite number of jointly distributed variables, the GP is simply a Gaussian distribution with an infinite number of variables, representing every possible point on the path.

Gaussian: P(x) = N(x; mean, variance)

Gaussian process: P(path) = GP(path; mean path, covariance function)


The most important property of a GP is that any subset of points on the path (such as the recorded positions from the GPS device - don't confuse GPs and GPS!) follow a multivariate Gaussian distribution,

P(recorded positions) = N(recorded positions, mean positions, covariance matrix)


We'll discuss more about exactly what the covariance matrix and mean positions represent in the next post.

Great! We're on our way. If we can assign probabilities to paths in a consistent manner we can ask if observed paths are more or less likely based on different hypotheses, which allows us to use data to select between those hypotheses. In the next post I'll give a rundown of the properties of GPs and how they work.

[In a switch of textbook, for these pigeon navigation posts I'll be advising you to look at the definitive guide to GPs, Gaussian Processes for Machine Learning, by Rasmussen and Williams, and what I have to assume is the definitive work on using GPs to analyse pigeon flight paths, Prediction of Homing Pigeon Flight Paths using Gaussian Processes, by one R. P. Mann]