Each of these aspects of data-driven healthcare has promise, but also problems. It is very difficult to reliably associate a disease or drug efficacy with a small number of testable gene alleles, and very easy to identify false positive gene associations. Routinely collected data is very difficult to make reliable inferences from in terms of cause and effect, because treatments are not randomly assigned to patients. Sophisticated analytics do not stop you needing to think about how your data was collected. Lifestyle optimisation via smartphones probably owes more to Silicon Valley's ideal of the hyper-optimised individual and a corporate desire for ever more personal data than any real health benefits beyond an increased motivation to exercise.
However, there are easy wins to be had from data. These are in prediction of future events that involve no medical intervention. It is difficult to predict how a drug will affect a patient, because you need to infer the drug's effect against a background of other potential causes. But it is much easier to tell if a patient arriving at the hospital for a specific operation will need to stay overnight; simply look at whether similar patients undergoing similar operations have done so. If this sounds exceptionally simple, that's because it is. However, the gains could be great. Hospitals routinely have to keep expensive beds available to deal with emergencies, or cancel planned operations to deal with unexpected bed shortages. A reliable system to estimate the length of patient stay after an operation with some accuracy would reduce the need for these expensive, time consuming and inconveniencing issues. On the ground staff already have a good sense for which patients will need to stay longer than others. However, in the maelstrom of an NHS hospital, anything that can help to systematise and automate the making and use of these estimates will reduce pressures on staff.
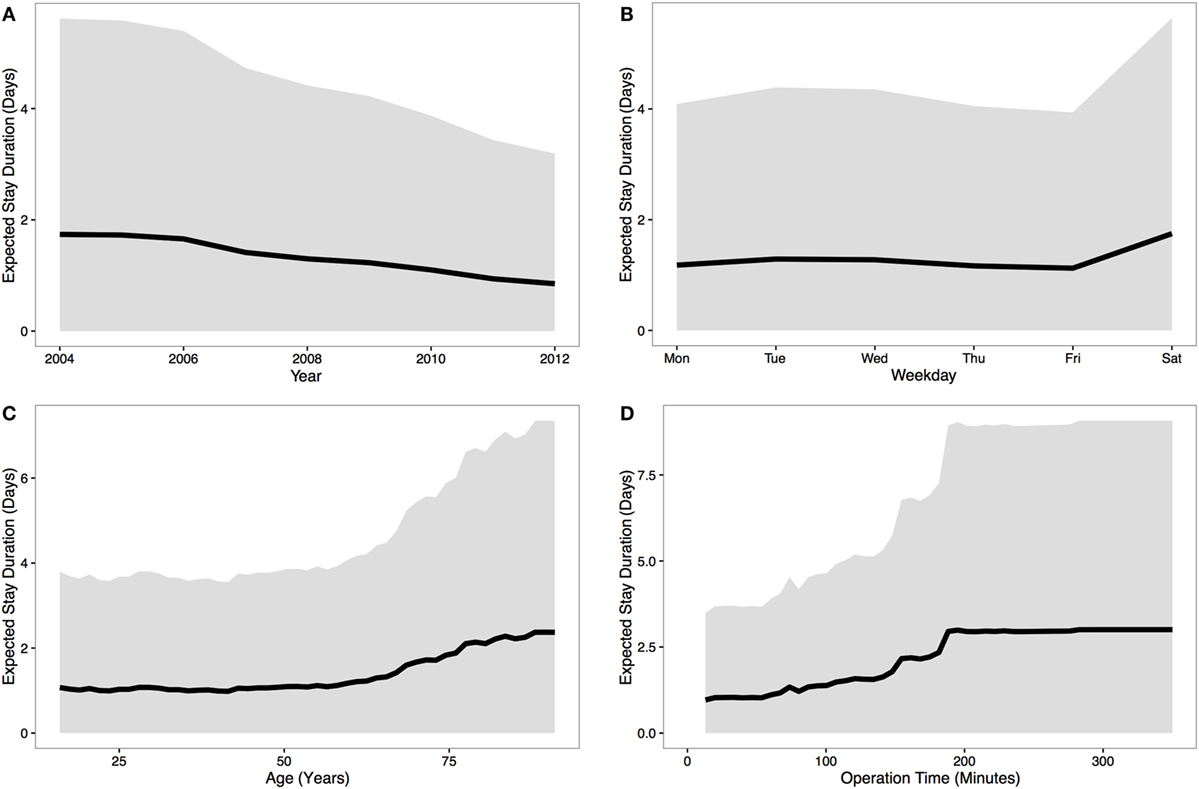
Exploring this possibility, we performed an analysis of data the NHS routinely collects for patients and procedures, such as age, year, day and surgery duration (see figure below), and used this to predict stay duration. Our results showed that a substantial portion of the variability in stay duration could be predicted from these data, which would translate to a significant saving for the NHS if generally applied and combined with current estimates of stay given by experts on the ground from their past experience. Note, importantly, we are not suggesting any intervention on the individual as a result of this analysis. For instance we make no judgement on whether the variation by day indicates anything important about treatment, only that this helps planners to know whats likely to come up next. This work is not about whether the NHS should operate a full weekend service!
As with numerical weather forecasts, we envisage this supplementing and supporting existing human expert judgement, rather than replacing it - there are clearly facets of the patient that we cannot capture in a simple data analysis. This provides a minimal cost use of existing data, with little or no complicating causal issues, that could save the NHS money on a daily basis. The size of the NHS means that small gains can be amplified on a national scale, while NHS data provides an enormous potential resource. It may be in these unglamorous aspects of healthcare provision that data analytics has immediate potential.